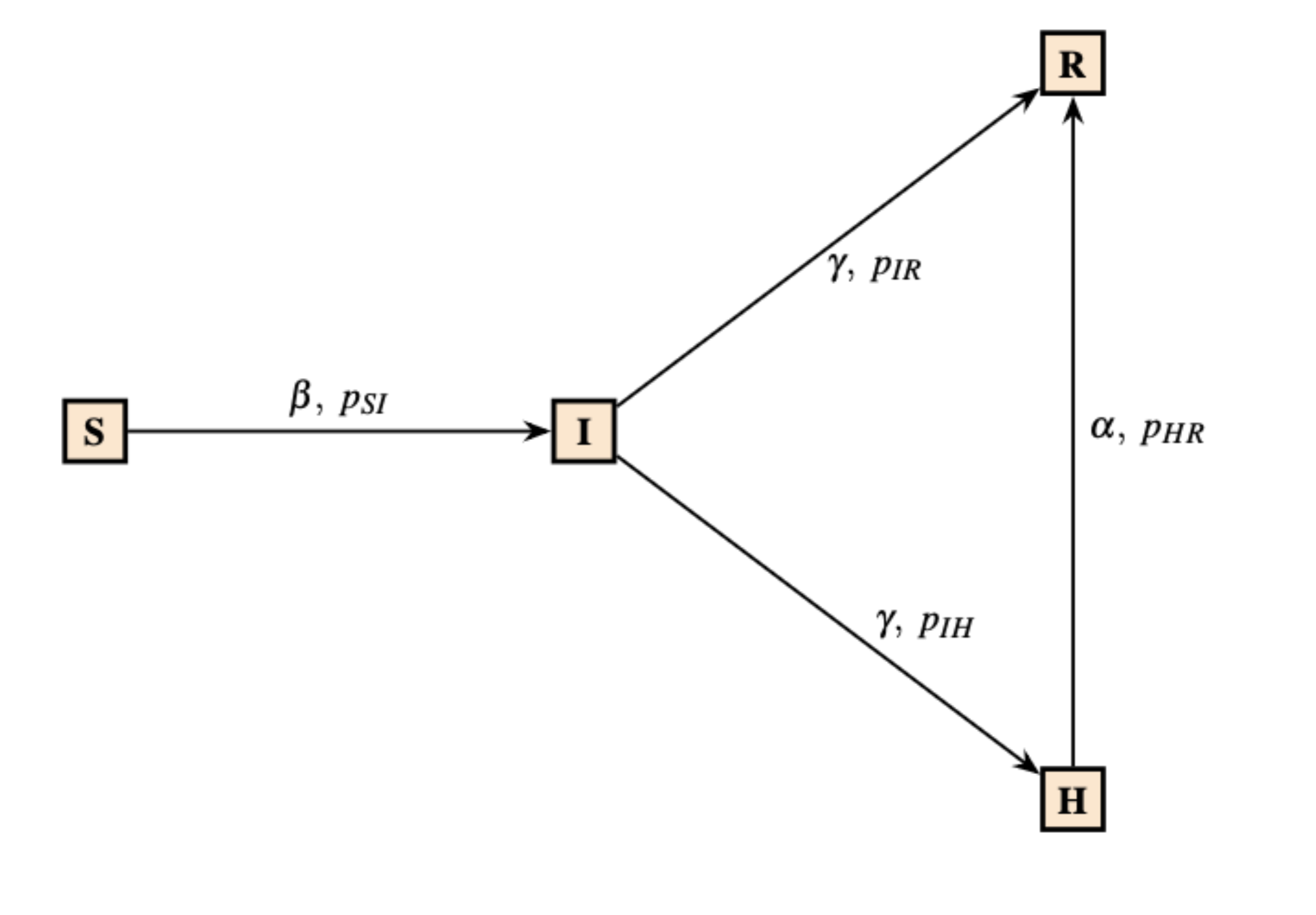
SIHR-IPC Model: System of ODEs
\[ \begin{align*} \frac{ds}{dt} &= -\beta p_{SI} s i \\ \frac{di}{dt} &= \beta p_{SI} s i - \gamma (1-p_{II}) i \\ \frac{dh}{dt} &= p_{IH} \gamma i - p_{HR} \alpha h \\ \frac{dr}{dt} &= p_{IR} \gamma i + p_{HR} \alpha h \end{align*} \]
- s: Susceptible proportion
- i: Infected proportion
- h: Hospitalized proportion
- r: Recovered proportion
- β, γ, α: rates
- pSI: S→I probability
- pII: I→I probability (remains infected)
- pIH: I→H probability
- pIR: I→R probability
- pHR: H→R probability
- pHH: H→H probability (remains hospitalized)
- Constraints: pIH + pIR + pII = 1, pHR + pHH = 1
Hospitalization Pattern Classification
The SIHR-IPC model's hospitalized population \( h(t) \) exhibits diminishing (monotonically decreasing), viral (initially increasing, then decreasing after a peak), or outbreak (initially decreasing, then increasing to a peak, then decreasing) behavior, determined by:
\[ \sigma_0 = s_0 \frac{\beta p_{SI}}{\gamma (1-p_{II})}, \quad \tilde{\sigma}_0 = \frac{\gamma p_{IH} i_0}{\alpha p_{HR} h_0}, \quad \tilde{\tilde{\sigma}}_0 = \frac{\gamma p_{IH} i(t_{p,i})}{\alpha p_{HR} h(t_{p,i})} \] where \( t_{p,i} \) is the peak time of \( i \).
Now we categorize the outcomes of \( h \) as: